浅析TreeMap

TreeMap虽然并不常用，但也是Java集合框架中一个重要的成员，在需要保证集合中成员有序时，它可以很好的发挥作用。TreeMap底层是基于红黑树实现的，它的增删查其实就是红黑树的增删查。但笔者这里并不打算详细介绍红黑树，因为红黑树的操作很复杂，特别是增删时需要对树进行多次旋转，并可能需要改变节点的颜色，以此来保证树的平衡并使之符合红黑树的定义。因此这片博客中笔者只是浅尝辄止，对TreeMap的源码进行简单分析。本文源码基于JDK1.8。JDK1.8开始虽然对TreeMap的源码进行了些许改变，但改变不大，底层原理不变。

概览

TreeMap的类的定义如下：

1
2
3

public class TreeMap<K,V>
    extends AbstractMap<K,V>
    implements NavigableMap<K,V>, Cloneable, java.io.Serializable

可见它继承了抽象类AbstractMap，并且实现了接口NavigableMap。AbstractMap这里就不说了，里面定义了Map的一些基本操作，常用的Map基本都继承了这个抽象类。而NavigableMap实现了接口SortedMap，是专门为有序Map服务的。因此TreeMap的继承结构可描述如下：

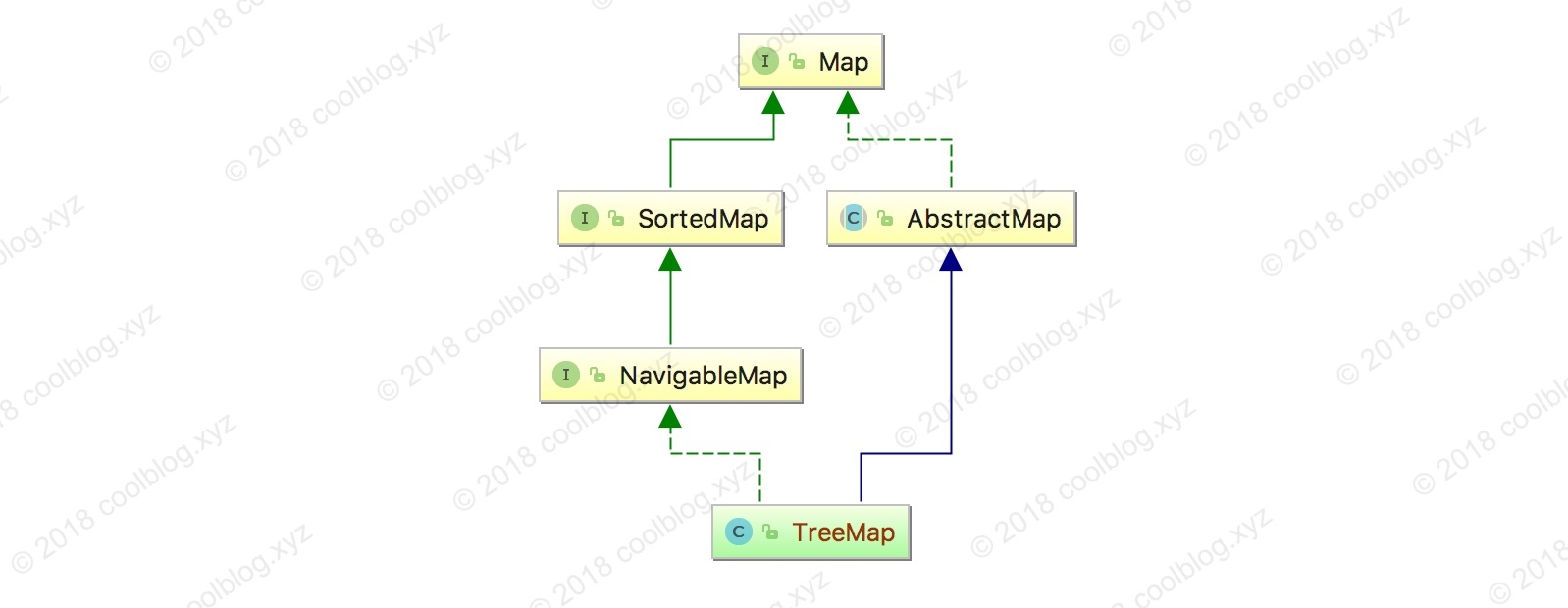
TreeMap有四个构造函数，如下：

1
2
3

public TreeMap() {
        comparator = null;
    }

1
2
3

public TreeMap(Comparator<? super K> comparator) {
        this.comparator = comparator;
    }

public TreeMap(Map<? extends K, ? extends V> m) {
    comparator = null;
    putAll(m);
}

public TreeMap(SortedMap<K, ? extends V> m) {
    comparator = m.comparator();
    try {
        buildFromSorted(m.size(), m.entrySet().iterator(), null, null);
    } catch (java.io.IOException cannotHappen) {
    } catch (ClassNotFoundException cannotHappen) {
    }
}

可能第一个和第二个比较常用一些。TreeMap有个成员变量comparator，作为排序时的比较器。第一个构造方法不指定比较器，此时集合中的元素会按照自然顺序排序，并且要求key必须实现Comparable接口。第二个构造函数指定一个外部的比较器，此时集合中的元素会使用这个比较器来排序，因此key不再需要实现Comparable接口。

既然是依托于红黑树实现的，那肯定一个节点类，用来存储数据。TreeMap的节点类也是一个实现了Map.Entry的Entry。结构如下：

static final class Entry<K,V> implements Map.Entry<K,V> {
        K key;
        V value;
        Entry<K,V> left;
        Entry<K,V> right;
        Entry<K,V> parent;
        boolean color = BLACK;

        /**
         * Make a new cell with given key, value, and parent, and with
         * {@code null} child links, and BLACK color.
         */
        Entry(K key, V value, Entry<K,V> parent) {
            this.key = key;
            this.value = value;
            this.parent = parent;
        }
        ......
}

可见这个Entry中除了存储数据的key，value外，还有表示节点颜色的color，及分别指向左右子节点的left，right，指向父节点的parent。

相关方法的实现逻辑

前面介绍了TreeMap的类结构信息及底层存储结构，下面介绍下TreeMap的工作原理，主要介绍下它的put（增改），remove（删），get（查）方法。

get方法

红黑树的查找其实就是二叉排序树的查找，逻辑比较简单。源码如下：

public V get(Object key) {
    Entry<K,V> p = getEntry(key);
    return (p==null ? null : p.value);
}

final Entry<K,V> getEntry(Object key) {
        // Offload comparator-based version for sake of performance
        if (comparator != null)
            return getEntryUsingComparator(key);
        if (key == null)
            throw new NullPointerException();
        @SuppressWarnings("unchecked")
            Comparable<? super K> k = (Comparable<? super K>) key;
        Entry<K,V> p = root;
        while (p != null) {
            int cmp = k.compareTo(p.key);
            if (cmp < 0)
                p = p.left;
            else if (cmp > 0)
                p = p.right;
            else
                return p;
        }
        return null;
    }

从代码可以看出，在查找时，首先判断内置的比较器comparator是否为空，如果不为空，则用这个比较器来查找元素；若该比较器为空则再次判断key是否为空，如为空，则抛出空指针异常，因此TreeMap中是不允许key为空的；然后，再采用key所实现的Comparable接口来遍历树查找所需要的Entry。最后，在put方法里判断在合格entry是否为null，若为空，则没查到，返回null；不为空，则返回value值。下面是使用传入的比较器查到的代码，逻辑是一样的：

final Entry<K,V> getEntryUsingComparator(Object key) {
        @SuppressWarnings("unchecked")
            K k = (K) key;
        Comparator<? super K> cpr = comparator;
        if (cpr != null) {
            Entry<K,V> p = root;
            while (p != null) {
                int cmp = cpr.compare(k, p.key);
                if (cmp < 0)
                    p = p.left;
                else if (cmp > 0)
                    p = p.right;
                else
                    return p;
            }
        }
        return null;
    }

put方法

put方法有点复杂，涉及到了红黑树的插入操作。而红黑树在插入时存在多种情况，并且可能需要旋转并更改节点的颜色。这里并不作深入介绍，反正就是插进去了，感兴趣的同学可以找些资料研究下红黑树的增删查。下面是put方法的源码：

public V put(K key, V value) {
        Entry<K,V> t = root;
        if (t == null) {
            compare(key, key); // type (and possibly null) check

            root = new Entry<>(key, value, null);
            size = 1;
            modCount++;
            return null;
        }
        int cmp;
        Entry<K,V> parent;
        // split comparator and comparable paths
        Comparator<? super K> cpr = comparator;
        if (cpr != null) {
            do {
                parent = t;
                cmp = cpr.compare(key, t.key);
                if (cmp < 0)
                    t = t.left;
                else if (cmp > 0)
                    t = t.right;
                else
                    return t.setValue(value);
            } while (t != null);
        }
        else {
            if (key == null)
                throw new NullPointerException();
            @SuppressWarnings("unchecked")
                Comparable<? super K> k = (Comparable<? super K>) key;
            do {
                parent = t;
                cmp = k.compareTo(t.key);
                if (cmp < 0)
                    t = t.left;
                else if (cmp > 0)
                    t = t.right;
                else
                    return t.setValue(value);
            } while (t != null);
        }
        Entry<K,V> e = new Entry<>(key, value, parent);
        if (cmp < 0)
            parent.left = e;
        else
            parent.right = e;
        fixAfterInsertion(e);
        size++;
        modCount++;
        return null;
    }

从代码可以看出TreeMap是在put时才开始初始化底层的节点结构的。逻辑大致分为以下几步：

判断根节点是否为空，若为空，初始化根节点，放入数据。并修改成员变量size（节点数），modCount（修改次数）。当然这里会做一下参数校验，检查参数是否为空。
根节点不为空，此时会检查比较器comparator是否为空，流程从这开始分叉；不为空则使用这个比较器，为空，则使用自然比较器。循环查找到插入位置，如果该值已经存在，则替换，返回旧值；如果不存在，找到插入位置的父节点。
插入节点，并调整树的结构，使之符合红黑树的定义，这些是fixAfterInsertion方法做的事。涉及到红黑树的操作，这里就不作介绍了。

remove方法

TreeMap的remove方法也涉及到红黑树的删除操作。红黑树的删除操作和插入操作一样很复杂，删除可能还要更复杂一些。因此这里也并不做红黑树删除的详细介绍。只看TreeMap的删除逻辑，其实很简单。下面是源码：

public V remove(Object key) {
        Entry<K,V> p = getEntry(key);
        if (p == null)
            return null;

        V oldValue = p.value;
        deleteEntry(p);
        return oldValue;
    }

从源码看，首先，它会查找这个entry，如果这个entry不存在，就返回空；若存在，删除这个entry，并返回旧值。其实主要操作都在deleteEntry这个方法里，这个方法会删除这个entry并重新平衡红黑石，使之重新符合红黑树的定义。

结束语

TreeMap虽然并不常用，但在某些场景中还是有有一些用武之地的。并且在一些面试中可能也会遇到，因此，还是需要花费一些时间来了解它的内部机制。本文只是做一些简单介绍，浅尝辄止。读者要想更深入的了解，还是需要了解一下红黑树的相关知识。